Dr. Peszynska says, “the overarching challenge in studying hydrates is arguably not just the complexity of the problem itself, but rather the ability to simplify and extract subproblems so as to move forward and make progress without compromising the results. For applied and computational mathematicians, the process of translating the hydrate model so it can fit into a mathematical framework amenable to analysis and simulation can be very rewarding. However, it requires vigilance from all participants of the interdisciplinary team, since the problem has many mathematical and computational sensitivities. Progressing from basin to production timescales, or from sediment depths to the scale of microcracks and gas chimneys, requires collaborations and resources across several fields. Observations and data are needed, so modeling can at least be guided even if validation is impossible.”
This research, funded by the National Science Foundation (NSF), has involved many of our mathematics graduate students including Joe Umhoefer, Choah Shin, and former students Tim Costa, Patricia Medina, and Ken Kennedy, as well as students outside mathematics such as Wei-Li Hong from CEOAS. Originally started in collaboration with CEAOS professors Marta Torres and Anne Trehu, the project involved many other Mathematics and CEOAS faculty including Ralph Showalter, Nathan Gibson, and Justin Webster.
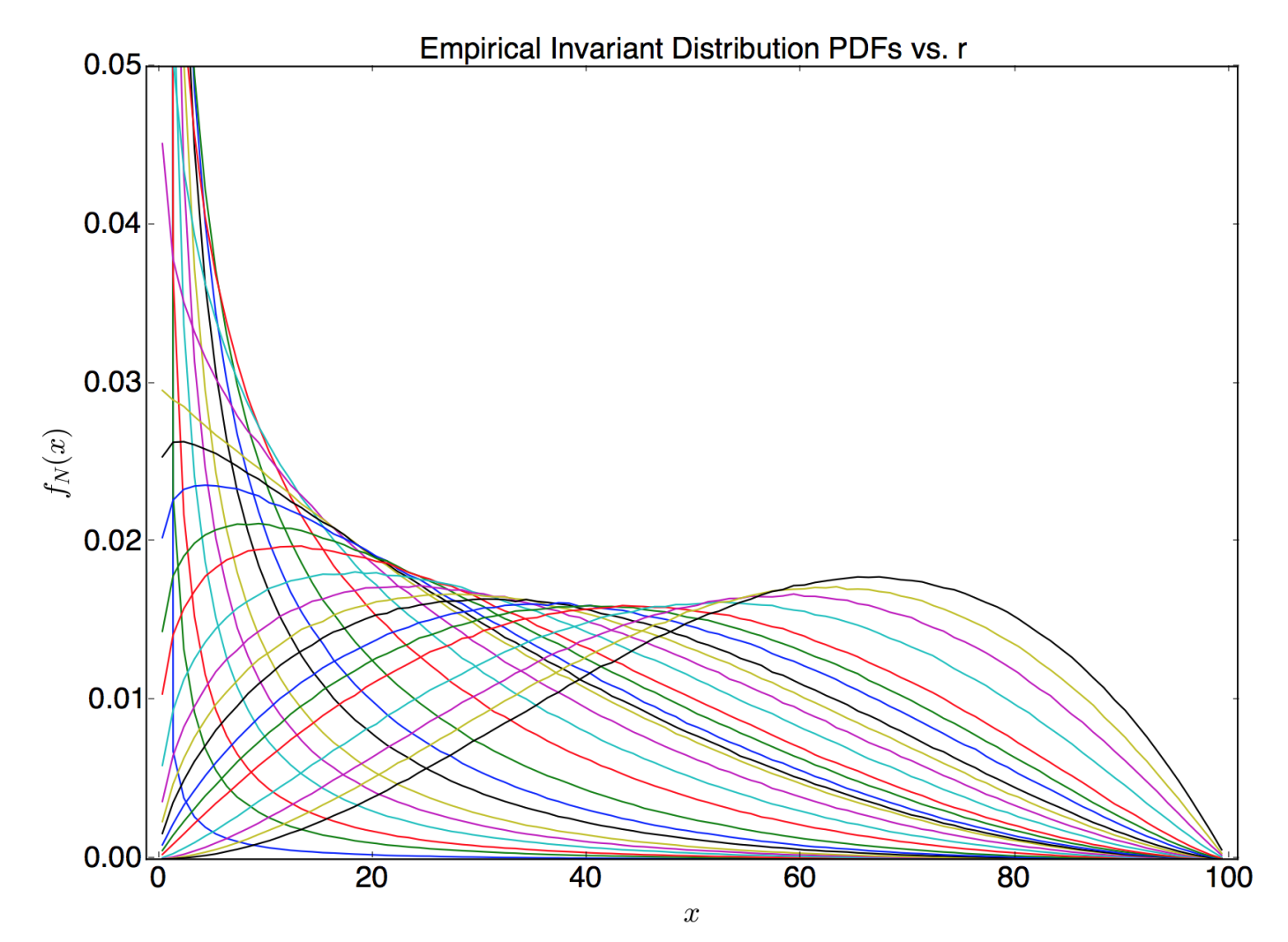
Understanding Random Distrubances in Populations: How can we construct a mathematical framework to understand how population-reducing events of varying frequency and intensity, like fires, floods, storms and droughts, can affect a species’ ability to survive? Mathematics Professor Patrick De Leenheer's collaborative work identifies “critical growth thresholds” for species subjected to random events that immediately and substantially impact the species’ population levels. The research was motivated in part to try to predict the effects of global climate change which may alter the characteristics of these events.
De Leenheer said, “Our main goal was to analyze when these models predict population extinction or persistence. We identified specific ecological and disturbance parameter combinations for which threshold values can be determined such that when these thresholds are crossed, the system’s extinction or persistence behavior changes fundamentally. That’s a key feature of these models. They provide precise conditions for which the mortality rate due to the frequency and magnitude of episodic disturbances exceeds the natural, net growth rate of a population. The thresholds mark a boundary between a persisting population of fluctuating size and one that becomes extinct at an exponentially fast rate.”